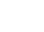圧力鍋はホントは「高温料理鍋」だった。ボルツマン分布の意味
昨晩、長女がLINEの「おやこ」グループに投稿しました。
友人の宿題(今朝が期限(笑))ならしいのですが、自分では刃が立たず、次女に助けを求めていました。某女子大の数物科学科の問題です。
見てみると、かなり興味深い。
・圧力鍋は圧力をかけることで水の沸点を上げている。ふつうは2気圧で120℃になっている
・これにより調理(熱分解反応など)スピードが3~4倍になる
と。
え、そうなんだ。圧力で調理しているわけでなくて、120℃という「高温」で調理を加速しているの!?
う~ん、流石にピンときません。たった20℃上がるだけで、料理スピード(=熱分解反応速度)が4倍にもなるの!?
絶対温度でいえば、100℃→120℃は、373K→393Kで、たった5.4%の増加に過ぎません。
それが、反応速度を4倍にあげるなんて…
ああ、でも違います。この世界は指数関数によって支配されているのでした。
もしexpXとexpYで、XとYに2倍の差があれば、その差は4倍になる!
これが、20℃高いとあっという間に煮上がり、20℃低いと永遠に煮上がらないヒミツでした。(この計算の詳細は下部で)
調べたら、常温帯では「10℃上がると反応速度が2倍になる」というアレニウスの法則、なんてものまでありました。
ふむふむ、なかなか勉強になったことでありました。
本当は、大学時代に、やったはずだがなあ……。
—————————————————————————————————-
以下は数学・物理好きの方向けです(笑)
問題文には、ご丁寧にボルツマン分布の式や解説が書いてあったりします。
そこから計算するのはちょっとおいておいて、まずはボルツマン分布について調べてみました。すると「アレニウスの式」なんてものがあり、問題文のそれとほぼ同等です。
左辺のkは反応速度を表します。
スウェーデンのスヴァンテ・アレニウスが1884年に提出した、ある温度での化学反応の速度を予測する式で、ヤコブス・ヘンリクス・ファント・ホッフによりこの式の物理学的根拠が与えられた、とWikipediaにはあります。
スウェーデンのスヴァンテ・アレニウスが1884年に提出した、ある温度での化学反応の速度を予測する式で、ヤコブス・ヘンリクス・ファント・ホッフによりこの式の物理学的根拠が与えられた、とWikipediaにはあります。
計算すると確かに常温帯では「10℃上がると反応速度が2倍」になります。なんと!
反応速度は、イコール、モノの劣化速度だったりするので、半導体などの世界で使用環境の温度が10℃下がると寿命は2倍に伸びるという「10℃2倍則」(=アレニウスの法則)として有名なようです。
「100℃で2000時間保つ」コンデンサがあったとして、それをいちいちテストしていたら3ヶ月もかかって大変です。なので、160℃にして何時間保つか調べるわけです。そこで250時間、つまり10日半保てば、「100℃で2000時間保つ」と言える。それがアレニウスの法則なのでした。
よくモノを高温にして劣化テストをやる(経年変化の加速試験)のですが、こういう裏付けがあったんですねえ。
さて話は圧力鍋に戻ります。
もともとの問題文にあるボルツマン分布の左辺は、P(E)でした。
分子ひとつがあるエネルギーE以上である確率です。それを越えると「反応する」ので、それが多いほど、反応速度はあがるわけです。
分子ひとつがあるエネルギーE以上である確率です。それを越えると「反応する」ので、それが多いほど、反応速度はあがるわけです。
20℃上がることで反応速度が4倍になるのが正しい、とすると、P(E)120℃=4 × P(E)100℃ ということになります。
P(E)120℃/P(E)100℃=4 であり、これは、exp(E/kB(1/373-1/393)))=4
与えられたkBボルツマン定数などから計算すると、E=1.40×10-19
与えられたkBボルツマン定数などから計算すると、E=1.40×10-19
ここから、
P(E)100℃=15.6%
P(E)120℃=62.3%
で、確かに、P(E)120℃がP(E)100℃の4倍になっていることがわかります。
P(E)100℃=15.6%
P(E)120℃=62.3%
で、確かに、P(E)120℃がP(E)100℃の4倍になっていることがわかります。
以上